Similarity measures and distances: Basic reference and examples for data science practitioners

WIP Alert This is a work in progress. Current information is correct but more content may be added in the future.

Euclidean distance

$$ \text{dist}(\vec{x},\vec{y})=\sqrt{\sum^n_{i=1} (x_i - y_i)^2} $$

• When to use

  • When you have normalized vectors.

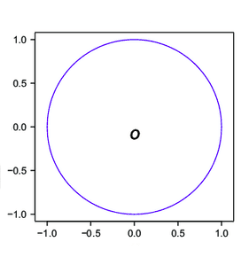All points in the blue circle have the same Euclidean distance to the origin.

Manhattan distance

Also called "city-block" distance

$$ \text{dist}(\vec{x},\vec{y})=\sum^n_{i=1} |x_i - y_i| $$

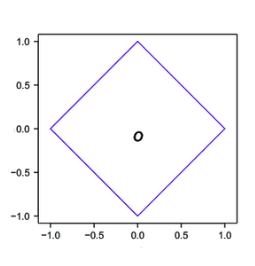All points in the blue square have the same Manhattan distance to the origin.

Mahalanobis distance

$$ \text{dist}(\vec{x},\vec{y})= \sqrt{(\vec{x} - \vec{y})' {\rm \bf C}^{-1} (\vec{x} - \vec{y}) } $$

where \(\vec{x}\) and \(\vec{y}\) are two points from the same distribution which has covariance matrix \({\rm \bf C}\).

The Mahalanobis distance takes into account how spread apart points are in the dataset (i.e. the variance of the dataset) to weigh the absolute distance from one point to another.

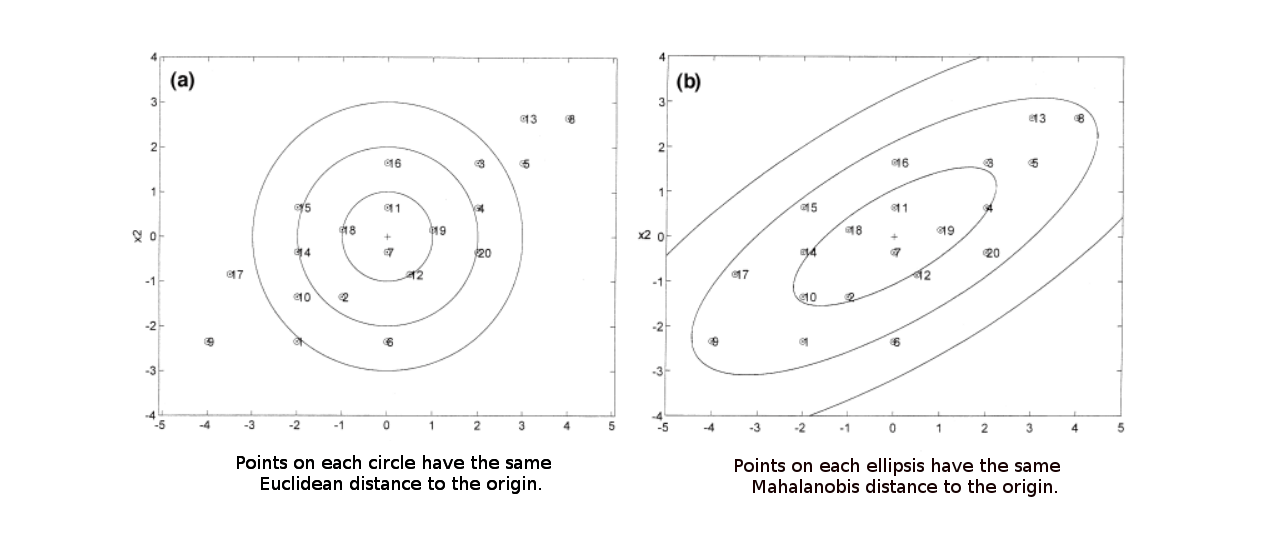For a very skewed dataset (such as the one shown on this picture),
the Mahalanobis distance (right) may be a better and more
intuitive distance metric.
Source: UWaterloo Stats Wiki

Intuitively: an absolute distance of 2 in a dataset that's very compact (i.e. low-variance) is more significant than an absolute distance of 2 in a dataset where points are normally very much apart from each other (i.e. high variance).

• When to use

  • When your points are correlated
  • When the covariance of the points is very far from spherical.

• Notes

  • The Mahalanobis distance corresponds to the Euclidean distance when the points are uncorrelated (i.e. when the covariance matrix is the identity matrix)

Cosine distance

$$ \text{dist}(\vec{x},\vec{y})=\frac{\vec{x} \bullet \vec{y}}{ \sqrt{\vec{x} \bullet \vec{x}} \sqrt{\vec{y} \bullet \vec{y}}} $$

where \(\bullet\) is the dot product between \(\vec{x}\) and \(\vec{y}\).

Cosine similarity measures the angle between two vectors in the vector space.

• When to use

  • When you do not want to take vector magnitudes into account, only their directions (for example, when using word frequencies to represent a document).

• Notes

  • Cosine distance is the same for normalized and unnormalized vectors.