Paper Summary: Large Margin Methods for Structured and Interdependent Output Variables
Last updated:Please note This post is mainly intended for my personal use. It is not peer-reviewed work and should not be taken as such.
WHAT
They extend the SVM learning algorithm in a way that enables it to use more general, arbitrary loss functions.
These functions are built to represent the mapping between input and structured output.
WHY
Previous attempts at designing algorithms to tackle this had some shortcomings.
Some were only really useful for a small subset of structured output problems. Some could not be used when the output space is large and some needed too much external information wrt. the shape of the output space to work.
HOW
After creating a problem-specfic loss function1 ,they formulate the problem as an adapted SVM problem by either re-scaling slack variables or margins in the original linear programming formulation for the algorithm.
Once the problem is formulated, they then propose a further improvement to the SVM optimization algorithm (so-called cutting-planes), whereby they prune out most constraints for each instance but still arrive at an approximate solution up to an error of ε (given).
CLAIMS
The proposed methods outperform methods where hard losses and other methods were used;
They applied a cutting-planes strategy to enable SVM to work with very large output spaces/constraints;
In each case where the method was demonstrated, it was claimed that other kernels (as in SVM) can also be used, which opens new avenues for improvements.
QUOTES
"... there always exists a polynomially sized subset of constraints so that the solution of the relaxed problem defined by this subset fulfills all constraints from the full optimization problem up to a precision of ε"
"... the algorithm can compute arbitrary close approximations to all SVM optimization problems posed in this paper in polynomial time for a large range of structures and loss functions."
Structured learning
Structured learning refers to when the output of the learning task is neither a real number (regression), a single class (classification) or even multiple classes (multiclass/multilabel learning), but structured objects such as:
Elements in a sequence
Nodes in a Tree-like structure
Nodes in a Graph
etc.
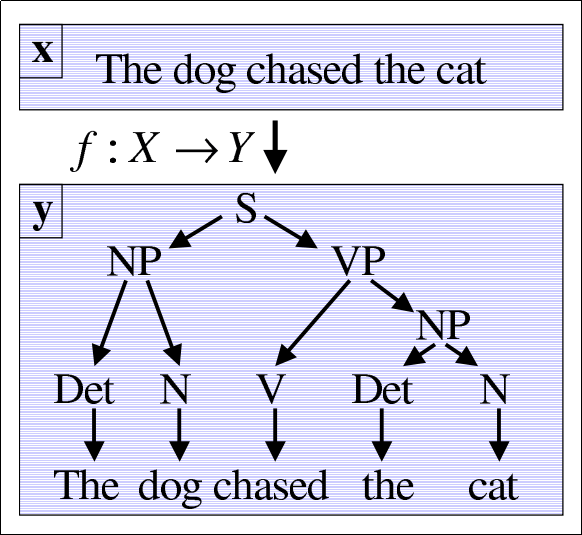Example of structured learning; The learning task consists in training a
model that produces a parse tree
given a textual phrase.
Source: Tsochantaridis et al. 2005
MY 2¢
It is an interesting approach inasmuch as it leverages a well-known and solid framework, namely SVMs, to the problem of structured learning, with all sorts of improvements.
However, it seems to me that writing a custom loss function for each problem may be hard/complex in some cases.
References
1: For example, a loss function for a parse tree (as in the image) could be a function that uses external information about which grammar rules are more likely in a given language. Then assign weights to each rule such that the inner product of the weights and the data produce more likely grammar rules.