Quick Reminder: Clustering

Traditional (non-hierachical) Clusters, such as K-Means:

Need to be given the number N of clusters and the initial cluster positions (centroids).

Hierarchical clusters

No need to inform number of clusters and positions, but you need to inform the linkage type.

Can be agglomerative (bottom-up) or divisive (top-down).

Linkage

It's the measure of dissimilarity (distance) between clusters.

• single linkage: distance between two groups is the smallest distance between two points in these groups.

  • elements at opposite ends of a cluster may be much farther from each other than to elements of other clusters.

• complete linkage: distance between two groups is the largest distance between two points in these groups.

  • Favours compact clusters with small diameters over long, straggly clusters.
  • Sensitive to outliers.

• average linkage: distance between two groups is the average distance between two points in these groups.

• ward linkage: distance between two groups is the difference between the sum of the squared distances of all points within each group.

  • Similar to K-means

Dendrograms

It's a way of representing hierarchical clusters.

Y-axis indicates dissimilarity.

E.g.,in the following picture:

• the dissimilarity between android and all other concepts is a little over 1600.

• the dissimilarity between php and javascript is around 1400.

• the dissimilarity between c# and java is a little over 1200.

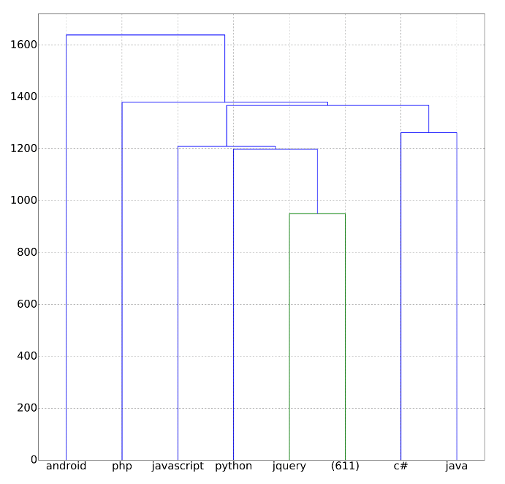Sample dendrogram (single linkage) of programming concepts.
Created using scipy.cluster.hierarchy.dendrogram

References

• Scikit-learn Docs: Clustering

Resources

• Hierarchical Clustering Notes

• Answer on Cross Validated: Overview of Linkage Methods

  • This lists several Linkage methods and useful "metaphors" on how to interpret them.

• Question on Cross Validated: Comparing hierarchical clustering dendrograms obtained by different distances & methods

  • One answer has 7 points to consider when experimenting with different metrics/linkage functions, written by a guy who is obviously quite knowledgeable on this topic.

• Scikit-learn Docs: Clustering with Different Metrics

  • A graphical example of the differences in outcomes when you use a metric that's invariant to scaling (such as cosine distance) on data that are proportional to one another.
  • Cosine distance just can't separate the data, even when there is absolutely no

• Scikit-learn Docs: Clustering with and without Structure

  • Graphical examples of the difference it makes when you add a connectivity constraint (such as forcing clustering to include only nearest neighours) to a clustering algorithm.
  • This is the same example, using 3D data