Features in Boosted Tree Algorithms: Engineering, Encoding, Interaction, etc
Last updated:Native feature interaction
"... If two variables X1 and X2 are used in different trees, but never in the same tree, then they do not interact: X1 can only affect the prediction through the trees it occurs in, and since X2 does not occur in these trees, the value of X2 cannot possibly affect the effect of X1, and vice versa." Goyal et al. 2007
Native1 feature interaction means that tree-boosting algorithms (as any tree-based algorithms) will naturally find ways to interact multiple feature values with each other.
This is because of the way decision tree algorithms work: A sequence of splits will be found, producing a label prediction at the end.
This is equivalent to interacting features with and-operators:
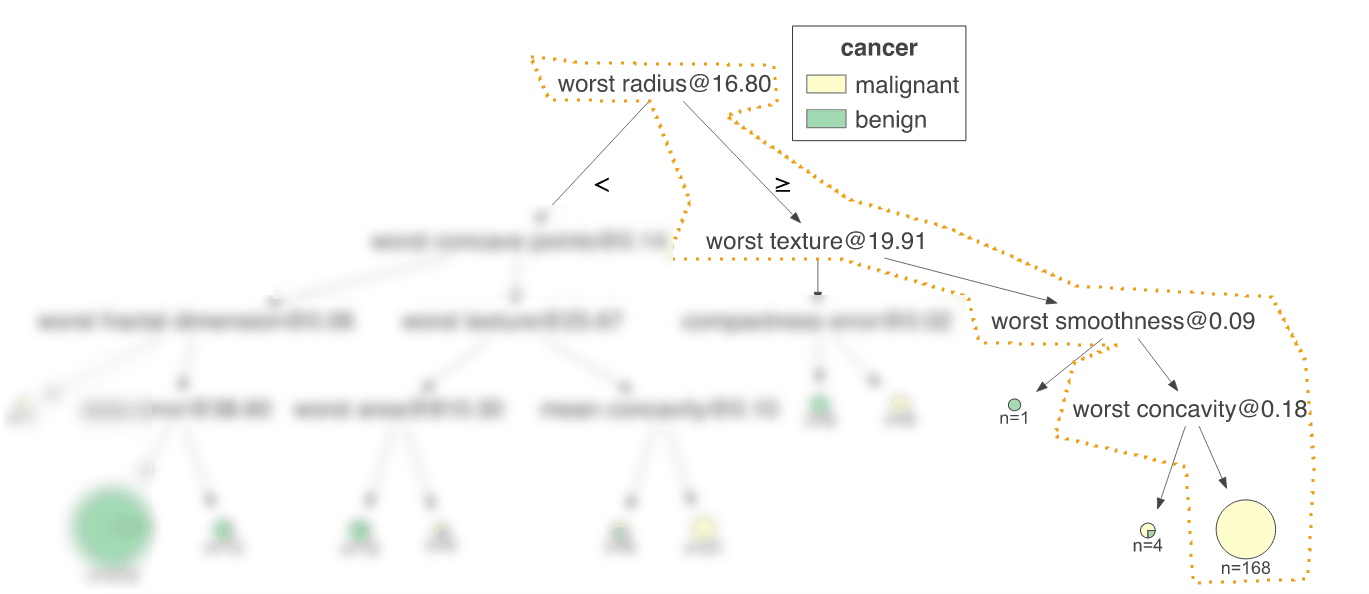
The path marked in orange above2 is equivalent to the following if/else structure:
IF (worst radius >= 16.80) AND (worst texture >= 19.91) AND (worst smoothness >= 0.09) AND (worst concavity >= 0.18) THEN cancer type is "malignant"
Interaction constraints
You can limit the features with which the algorithm will try to combine features in subsequent branches of the current tree: It's available in LightGBM and in XGBoost.
It's called interaction_constraints and takes a list of lists. Each list contains the features indices that should interact with each other.
But why would anyone want to restrict the space of interactable features?
May lead to better performance
Less noise and better generalization (OOS or OOT)
Regulatory issues
Custom feature engineering
Whenever we say aggregates we are referring to any of of aggregation operations such as: min, max, sum, count, count_distinct, sum, std_dev, variance
In addition to the native feature interaction done by tree-based algorithms, you will want to encode domain knowledge via custom engineered features so that the algorithm can learn from these.
Needless to say, be careful to not leak information from the future or from the test set when grouping data to perform aggregations on.
Here are some examples of ways to engineer features for use with tree-based algorithms:
Basic operations: addition, subtraction, division, min, max
- Example: Create a new feature by dividing one numeric feature another. Add two features, subtract one from the other. Also, take the minimum or the maximum among two features
- Use case: In any situation where there are multiple numeric features you can combine. Ratios are useful to add a "relative" perspective to absolute values
Apply smoothing transformations to numeric features
- Example: Log smoothing, for example using the following formula smoothed_value = log(1 + original_value)
- Use case: When there are features that have a very large range (i.e. things that follow power laws and may be either very large or zero)
Decompose temporal features into periods
- Example: Event count in the last (30 days, 15 days, 1 day, 12 hours, etc), also create ratios (event count in the last 1 day divided by the event count in the last 30 days). Also min, max, avg of values of a feature in a period.
- Use case: In any situation where you have timestamped features, it's possible to engineer lots of derived information from them
Geographical features
- Example: Basically distances, such as distance between current coordinates and some other fixed point.
- Use case: You will most likely use this in real-time models, where you have the current position of the data point during inference time.
Aggregated features over a group
- Example: Suppose you have a dataset where each row is a credit card application and you have an auxiliary dataset with the purchases that person has made in their savings account. Create features such as average amount of purchases of groceries in the last 30 days
- Use case: Any situation where you have extra information with categories you can group and get aggregated values such as sum, count, min, max, avg, etc.
Aggregated features over location
- Example: mean, min, max of some feature in a geographical area within X miles of the coordinates where the current data point is. Number of times the current user has been within Y miles of some other fixed point.
- Use case: Again, usually for real-time models, where the current position of the data point is available at inference time.
Types of categorical feature encoding
Any encoding needs to be replicated exactly in train/test sets and also when monitoring a model in production.
LightGBM provides out-of-the-box support for categorical features, using the categorical_features configuration parameter
Correctly encoding categorical features is important for the tree-boosting algorithm to be able to efficiently learn from these:
| Description | Application in Tree Boosting algorithms |
|
|---|---|---|
| One-hot encoding | Simplest encoding, one dimension per category value | Not recommended for tree boosting algorithms because it is inefficient and hard for the algorithm to use values like these to create branches. |
| Numeric encoding | Assigning a random number to each possible category value | Same as above |
| Hash encoding | A deterministic function takes all category values and compresses them into a fixed-width array that summarizes the information.
(Saves space at the cost of hash collisions) |
Same as above |
| Target encoding | Replace the category value c with the mean of the target in all rows where the category equals c | This is usually the preferred method for Gradient Boosting |
1: Native feature interaction stands opposed to hand-crafted features built by hand based on the values of other features, such as you creating a feature \(C = \frac{A}{B}\) based on the values of \(A\) and \(B\).
2: Image generated with dtreeviz