Choosing C Hyperparameter for SVM Classifiers: Examples with Scikit-Learn
Last updated:- SVM tries to find separating planes
- Kernel methods
- Noisy points
- Soft-margin vs hard-margin
- The C parameter
- Examples: Generating synthetic datasets for the examples
- Examples: Choice of C for SVM Linear Kernel
- Examples: Choice of C for SVM, Polynomial Kernel
- Examples: Choice of C for SVM, RBF Kernel
TL;DR: Use a lower setting for
C(e.g. 0.001) if your training data is very noisy. For polynomial and RBF kernels, this makes a lot of difference. Not so much for linear kernels.
View all code on this jupyter notebook
SVM tries to find separating planes
In other words, it tries to find planes that separate Positive from Negative points
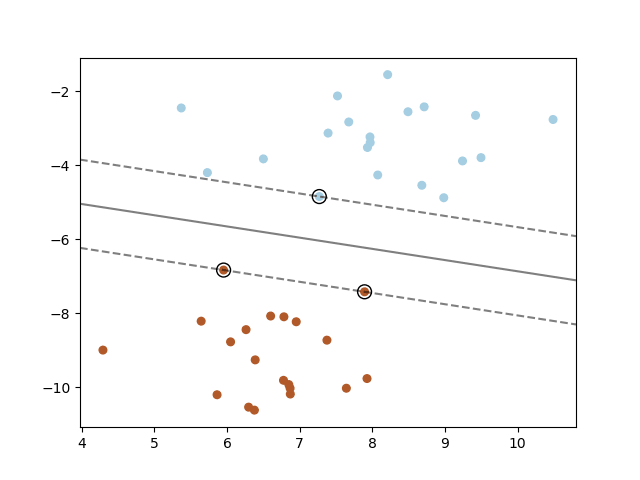 The solid line in the middle represents the best possible line for separating positive from negative samples.
The solid line in the middle represents the best possible line for separating positive from negative samples. The circled points are the support vectors.
Source: Sklearn Guide on SVMs
Kernel methods
SVM can also find surfaces other than simple planes if you employ kernel methods
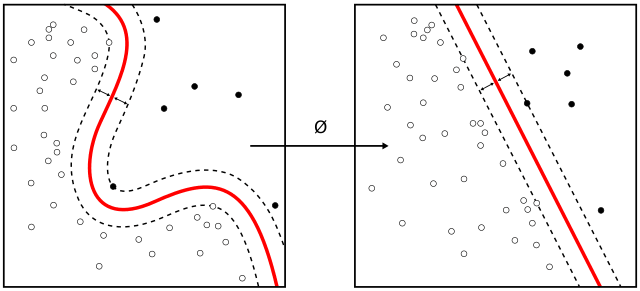 Kernels (transformation functions) can be used to transform
Kernels (transformation functions) can be used to transform the points such that hyperplanes can be found even for points that are not
linearly separable
Source: Wikipedia Article on Kernel Methods
Noisy points
Real-life data is noisy, so a robust SVM classifier must be able to ignore noisy, outlier points to discover a generalizable plane.
Soft-margin vs hard-margin
| Hard-margin SVM | Soft-Margin SVM |
|---|---|
| Try to find a hyperplane that best separates positive from negative points, such that no point is misclassified. |
Try to find a hyperplane that best separates positive from negative points, but allows for some points to be misclassified, in which case the objective function is punished proportionally to degree of misclassification |
By default, most packages like scikit-learn implement a soft-margin SVM.
This means that a separating hyperplane that separates positive from negative points will still be considered even if some points are misclassified.
The C parameter
The lower the C parameters, the softer the margin
The C parameter controls how much you want to punish your model for each misclassified point for a given curve:
| Large values of C | Small Values of C |
|---|---|
| Large effect of noisy points. A plane with very few misclassifications will be given precedence. |
Low effect of noisy points. Planes that separate the points well will be found, even if there are some misclassifications |
In other words, C is a regularization parameter for SVMs.
Examples: Generating synthetic datasets for the examples
More information on creating synthetic datasets here: Scikit-Learn examples: Making Dummy Datasets
For all the following examples, a noisy classification problem was created as follows:
We generated a dummy training dataset setting
flip_yto 0.35, which means that in this dataset, 35% of the targets are flipped, i.e. a 1 where a 0 should be and a 0 where there should be a 1We generated a dummy test dataset with the same settings as the training dataset, except for the noise parameter (
flip_y). There is no noise in the test dataset because we want to ascertain how much a model trained on noisy data performs with respect to the choice of C.
np.random.seed(222)
# train dataset
X, y = make_classification(
n_samples=10000,
n_features=10,
n_informative=10,
n_redundant=0,
weights=[0.3,0.7],
class_sep=0.7,
flip_y=0.35) # the default value for flip_y is 0.01, or 1%
X_train, _ , y_train, _ = train_test_split(X, y, test_size=0.25)
np.random.seed(222)
# test dataset
X, y = make_classification(
n_samples=10000,
n_features=10,
n_informative=10,
n_redundant=0,
weights=[0.3,0.7],
class_sep=0.7,
flip_y=0.0)
_, X_test , _ , y_test = train_test_split(X, y, test_size=0.25)
Examples: Choice of C for SVM Linear Kernel
For a linear kernel, the choice of C does not seem to affect performance very much:
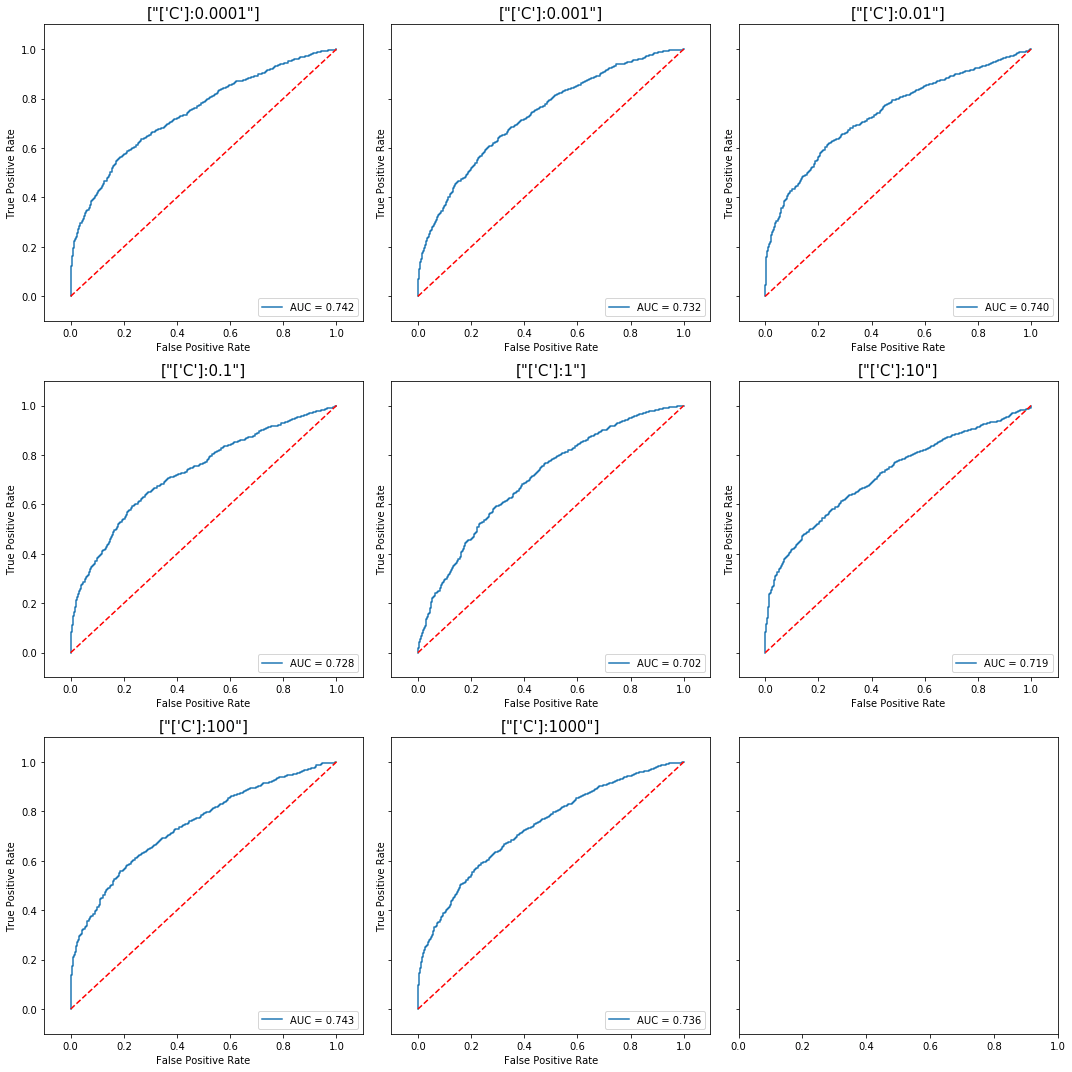 For a linear kernel, varying the C parameter doesn't make much difference
For a linear kernel, varying the C parameter doesn't make much difference even though we are using a highly noisy dataset.
View the full code here: linear-kernel
Examples: Choice of C for SVM, Polynomial Kernel
For polynomial kernels, the choice of C does affect the out-of-sample performance, but the optimal value for C may not necessarily be the lowest one.
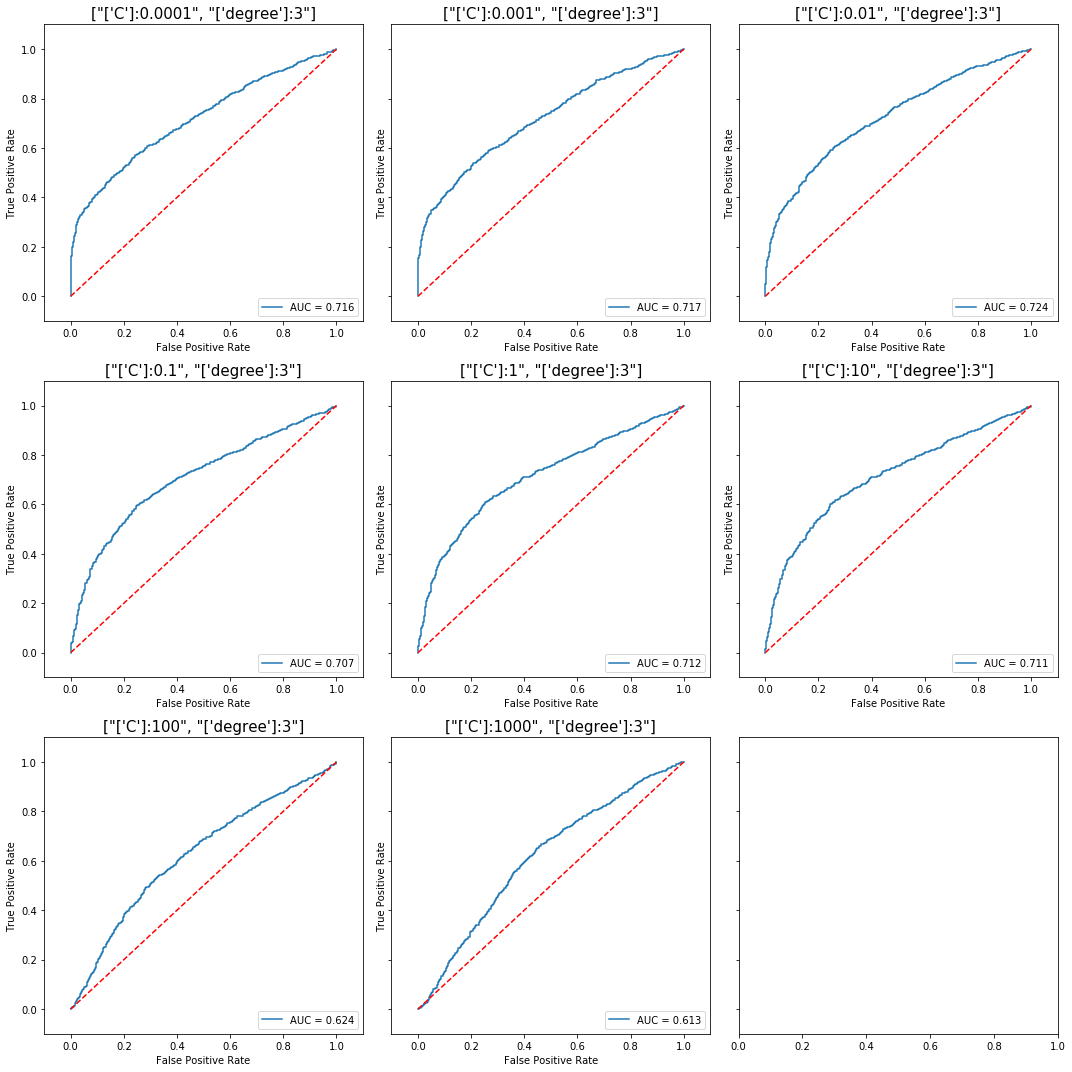 For a polynomial kernel with degree 3, there's a clear pattern of lower
For a polynomial kernel with degree 3, there's a clear pattern of lower performances with higher values of C, but the best value for out-of-sample
score was not achieved at the minimum C, but with C=0.01.
View the full code here: polynomial kernel, degree=3
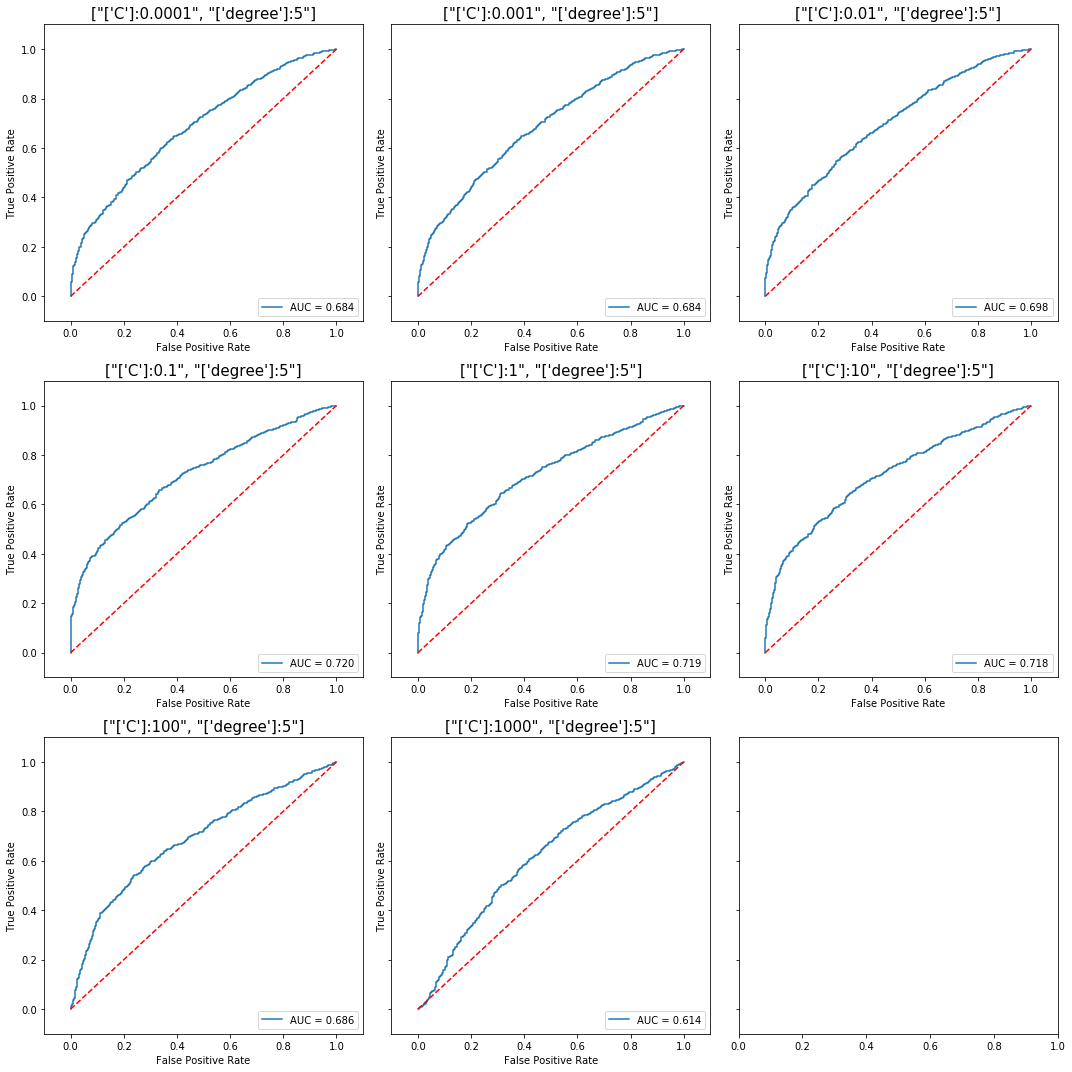 Again, for a polynomial kernel with degree 5, the optimal value for out-of-sample score
Again, for a polynomial kernel with degree 5, the optimal value for out-of-sample score was not achieved at the minimum C, but with C=1.0.
View the full code here: polynomial kernel, degree=5
Examples: Choice of C for SVM, RBF Kernel
For an SVM model with the RBF kernel, it is once more easy to see that lower values of the C parameter allow the classifier to learn better under noisy data.
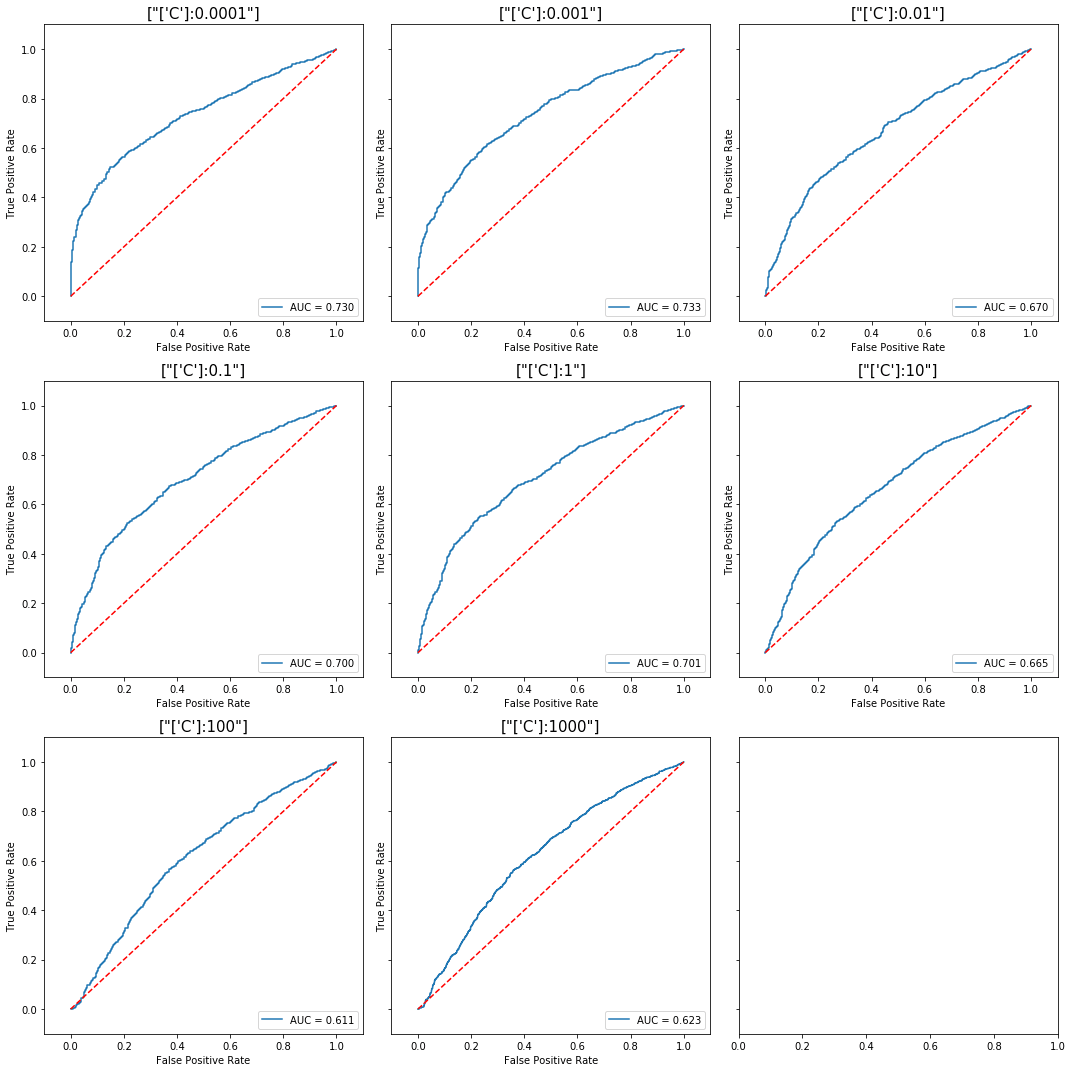 Difference in performance for a SVM trained
Difference in performance for a SVM trained using the RBF kernel, with varying choice of C.
View the full code here: RBF kernel
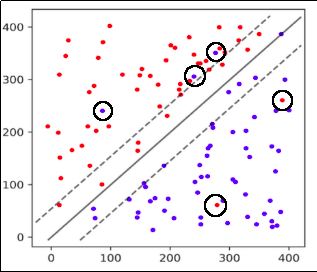 A separating plane that ignores some (probably noisy) points.
A separating plane that ignores some (probably noisy) points.